Morris Inorder Tree Traversal

2018-04-20

• algorithm

---

Content:

1. Problem statement

Given a binary tree, print its node values in inorder traversal.

Let’s call N is the number of nodes in tree.

Morris algorithm can solve this problem in $O(N)$ time complexity and $O(1)$ space complexity.

---

Figure 1. Inorder of this binary (search) tree is 1 3 4 6 7 8 10 13 14
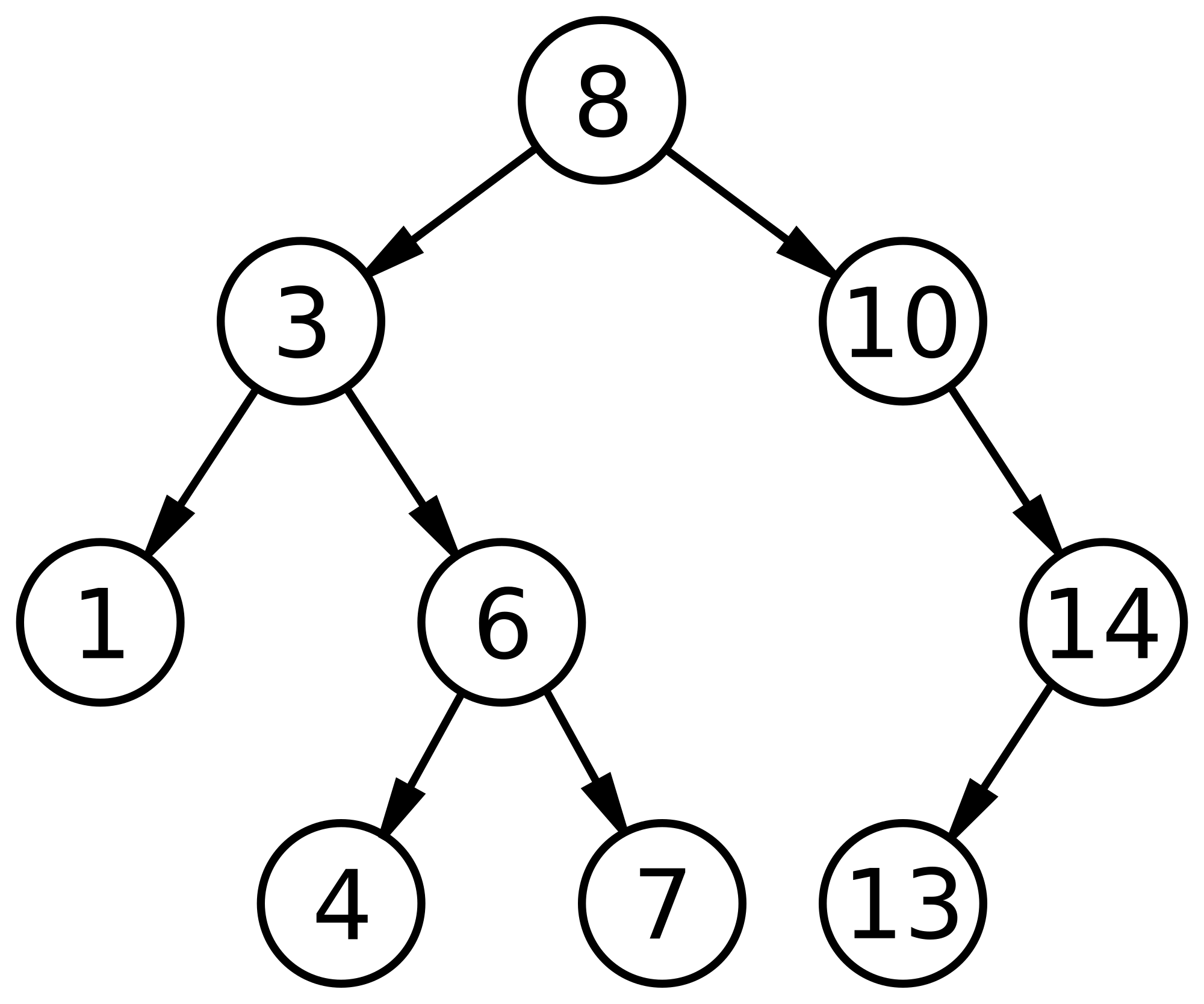
(Source: Wikipedia - Binary tree)

---

2. Solution

Let’s call H is the height of tree.

Since there is no way a recursive implementation can give us a O(1) space complexity solution, we’re gonna approach the iterative way.

In normal inorder traversal algorithm, we use a stack to save the nodes to which we need to visit later (i.e. the inorder tree traversal is left, root, right, when we’re about to visit the left sub tree, we need to store the root node in the stack to return to it later). Because of the stack, we have a $O(H)$ space complexity algorithm.

So in order to reduce the space complexity, we need a way to return to the root node after visiting its left sub tree without storing it.

Morris algorithm has these following intuitions:

• To return to the root node, we can create a link from some node (let’s cal it p) in its left sub tree to it. Further more, to avoid breaking the tree structure, we can utilize the x nodes whose left (or right) child is NULL (i.e. if x->left == NULL (or x->right == NULL) we can link it to the root: x->left = root (or x->right = root).
• It would be natural if we choose the node p so that it comes right before its root node in inorder tree traversal (let’s call p is predecessor node of its root node), further more the left child of this p node is also NULL. For example in Figure 1, we can link: 1->left = 3, 4->left = 6, 7->left = 8 and so on.

3. Implementation

TreeNode* getPredecessor(TreeNode* node) {
  TreeNode* p = node->left;
  while(p->right != NULL && p->right != node) {
    p = p->right;
  }
  return p;
}

void morris_inorder(TreeNode* root) {
  TreeNode* node = root;
  // While node is sill not the last node
  while(node != NULL) {
    // If this node has no left child, we visit it
    // and continue traversing to its right child.
    // This is also probably the link that we had
    // created before to return to its root node
    if (node->left == NULL) {
      print("%d ", node->val);
      node = node->right;
    } else {
      // Otherwise, we first need to get the
      // predecessor of current node
      TreeNode* p = getPredecessor(node);

      // If we haven't created the link yet,
      // create it (so that we can get back
      // later) and then can safely continue
      // traversing the left child
      if (p->right == NULL) {
        p->right = node;
        node = node->left;
      } else {
        // Otherwise if the link had already
        // created, we know that the left
        // child of current node had already
        // visited; we now can visit the node
        // and move to its right child.
        print("%d ", node->val);
        node = node->right;
        p->right = NULL;  // remove link
      }
    }
  }
}

• Time complexity: there are 2 types of nodes here, the nodes we need to create the link from some node in its left child back to it (i.e. the nodes which have left child) and the nodes we no need to create a link (i.e. the nodes which don’t have left child). Let’s call the number of the first type is N1, so the number of second type is N - N1.
  • We need to visit each of first type node twice and each of second type node once, thus the time complexity is $O(2N1 + N - N1) = O(N + N1)$.
  • With each node of the first type, we need to call getPredecessor twice (one for creating link and one for removing it). The sets of edge that this function iterates through for each first-type node don’t intersect each other, and their union is the number of edge in the binary tree, which is N - 1. So the time complexity here is $O(2(N-1))$.
  • Total time complexity is $O(N+N1) + O(2(N-1)) = O(3N + N1 -2) = O(3N + N1)$, in worst case $N1 \approx N$, thus the time complexity is $O(3N + N) = O(4N) = O(N)$ in worst case.
  • Conclusion: time complexity is $O(N)$ in every case.
• Space complexity: $ O(1)$.

« Postorder traversal on binary tree Binary tree iterators »