Inorder traversal on binary tree
2018-04-19Content:
1. Problem statement
Given a binary tree, print its node values in inorder traversal.
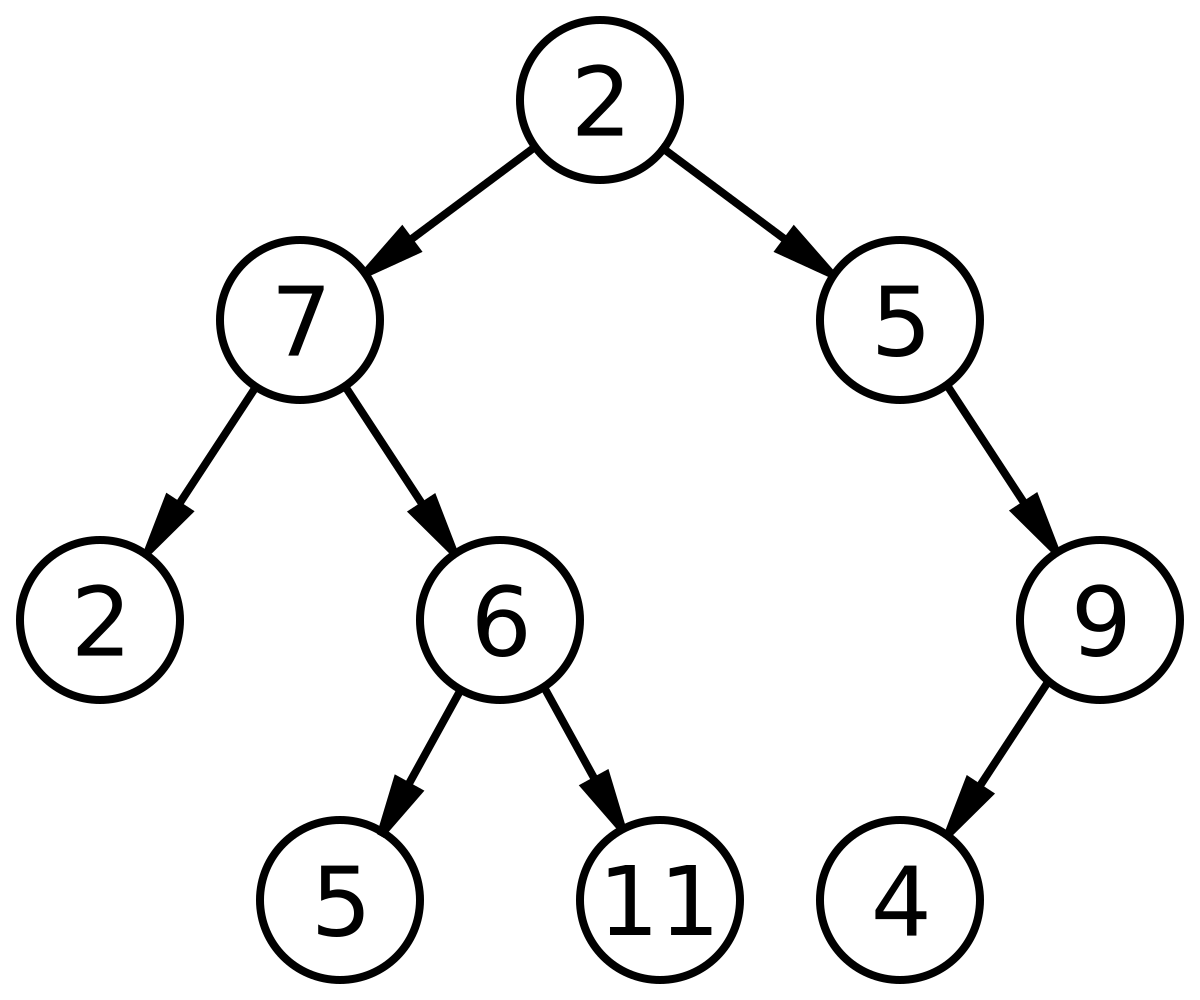
Figure 1. Inorder of this binary tree is 2 7 5 6 11 5 4 9
(Source: Wikipedia - Binary tree)
(Source: Wikipedia - Binary tree)
2. Solution
Inorder traversal means we visit the tree in left, root, right order: the left node is visited first, then the root the right child (thus the word in).
3. Implementation
3.1. Recursion
1
2
3
4
5
6
7
void inorder(TreeNode* root) {
if (root == NULL) return;
inorder(root->left);
print("%d ", root->val);
inorder(root->right);
}
Let’s call N is the number of nodes, H is the height of the tree.
- Time complexity: $ O(N)$ since each node is visited exactly once.
- Space complexity: $ O(H)$, the call stack can reach
Hin depth and each recursive call needs $ O(1)$ to store its parameters.
3.2. Iteration
Solution 1: (more intuitive)
1
2
3
4
5
6
7
8
9
10
11
12
13
void inorder(TreeNode* root) {
stack<TreeNode*> stack();
TreeNode* node = root;
while(!stack.empty() || node != NULL) {
while(node != NULL) {
stack.push(node);
node = node->left;
}
node = stack.top(); stack.pop();
print(node->val);
node = node->right;
}
}
Solution 2:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
void inorder(TreeNode* root) {
stack<TreeNode*> stack();
TreeNode* node = root;
while(!stack.empty() || node != NULL) {
if (node != NULL) {
stack.push(node);
node = node->left;
} else {
node = stack.top(); stack.pop();
print(node->val);
node = node->right;
}
}
}
- Time complexity: $ O(N)$ since each node is visited exactly once.
- Space complexity: space complexity is the maximum size of
stack. On a path from root to some node, easily observe that the stack need to store all of nodes on that path. Thus the space complexity is $ O(H)$.
4. Properties
- Inorder traversal on a binary search tree will return a increasing array order.
