Selection sort

2018-04-22

Content:

1. The idea

Say we want to sort an array in ascending order, N = length of array

The selection sort algorithm’s idea is that first we find the smallest element and move it to the front of the array, then find the 2nd smallest element move it, keep doing that until the array is sorted.

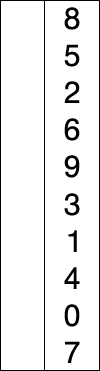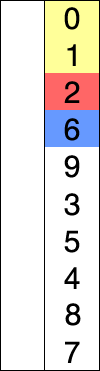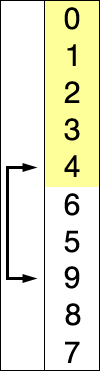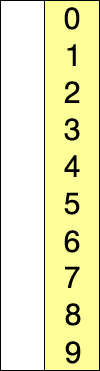
Figure 1. Selection sort visualization
(Source: Wikipedia - Selection sort)

The selection sort is similar to the bubble sort, they’re just different in how the next element is found:

  • In bubble sort, this’s done by swapping.
  • In selection sort, this’s done by selection (thus the name selection sort).

2. Implementation

1
2
3
4
5
6
7
8
9

void selection_sort(vector<int>& arr) {
  for(int k = 0; k < n-1; k++) {
    int minId = k;
    for(int i = k+1; k < n; k++)
      if (arr[i] < arr[minId])
        minId = i;
  }
  swap(arr[k], arr[minId]);
}

3. Complexity analysis

Let’s call N = length of the array.

Time complexity: Regardless of the initial array is sorted or not, time complexity of selection sort is always $O(N^2)$ (proof is similar to this.)

Space complexity: $ O(1)$.

4. Properties

  • The above implementation is not a stable one, but we can implement insertion sort as a stable sort by using an efficient data structure (like linked list) to squeeze the swapping step.