Preorder traversal on binary tree
2018-04-19Content:
1. Problem statement
Given a binary tree, print its node values in preorder traversal.
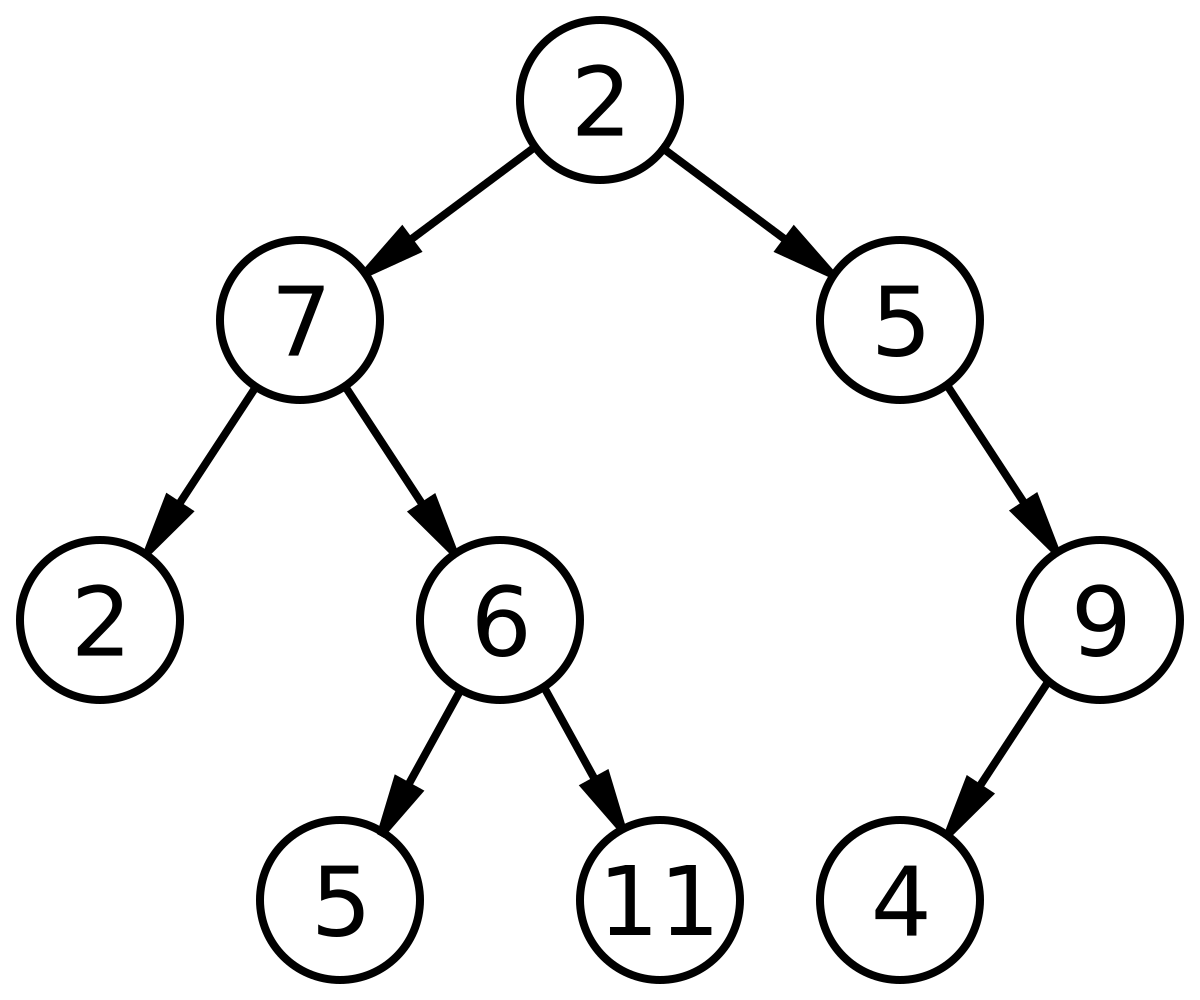
Figure 1. Preorder of this binary tree is 2 7 2 6 5 11 5 9 4
(Source: Wikipedia - Binary tree)
(Source: Wikipedia - Binary tree)
2. Solution
Preorder traversal means we visit the tree in root, left, right order: the root node is visited first (thus the word pre), then its left and right child.
3. Implementation
3.1. Recursion
1
2
3
4
5
6
7
void preorder(TreeNode* root) {
if (root == NULL) return;
print("%d ", root->val);
preorder(root->left);
preorder(root->right);
}
Let’s call N is the number of nodes, H is the height of the tree.
- Time complexity: $ O(N)$ since each node is visited exactly once.
- Space complexity: $ O(H)$, the call stack can reach
Hin depth and each recursive call needs $ O(1)$ to store its parameters.
3.2. Iteration
Using stack:
1
2
3
4
5
6
7
8
9
10
11
void preorder(TreeNode* root) {
stack<TreeNode*> stack({root});
while(!stack.empty()) {
TreeNode* node = stack.top();
stack.pop();
if (node == NULL) continue;
print("%d ", node->val); // visit node
stack.push(node->right); // push right first..
stack.push(node->left); // ..then push left, so that left is visited before right
}
}
- Time complexity: $ O(N)$ since each node is visited exactly once.
- Space complexity: Space complexity is the maximum size of
stack.- If the binary tree is skewed, space complexity will be $ O(1)$.
- Now imagine a binary tree is composed of complete left-skewed sub trees: for example the complete left-skewed sub trees (i.e. a path from root to leaf node by constantly turning left) of the binary tree in Figure 1 are
2 7 2,6 5,11,5,9 4. We can present any path from the root to some node as the form (not neccesarily complete) left-skewed sub tree, turn right, left-skewed sub tree, turn right..: for example the path from root2to leaf node5can be represented as2 7turn right6 5. Notice that on a path from root to some node, the stack will store the right child of nodes on the left-skewed trees (except for nodes where we turn right. In the worst case: this path will be a complete left-skewed sub stree, each node on this sub tree has a right child and the length of this sub tree isH, the space complexity is now $ O(H)$. - Conclusion: $ O(1)$ if the binary tree is skewed, $ O(H)$ in average and worst case.
4. Properties
- Two binary trees have the same structure if and only if they have the same preorder traversal.
