Postorder traversal on binary tree
2018-04-19Content:
1. Problem statement
Given a binary tree, print its node values in postorder traversal.
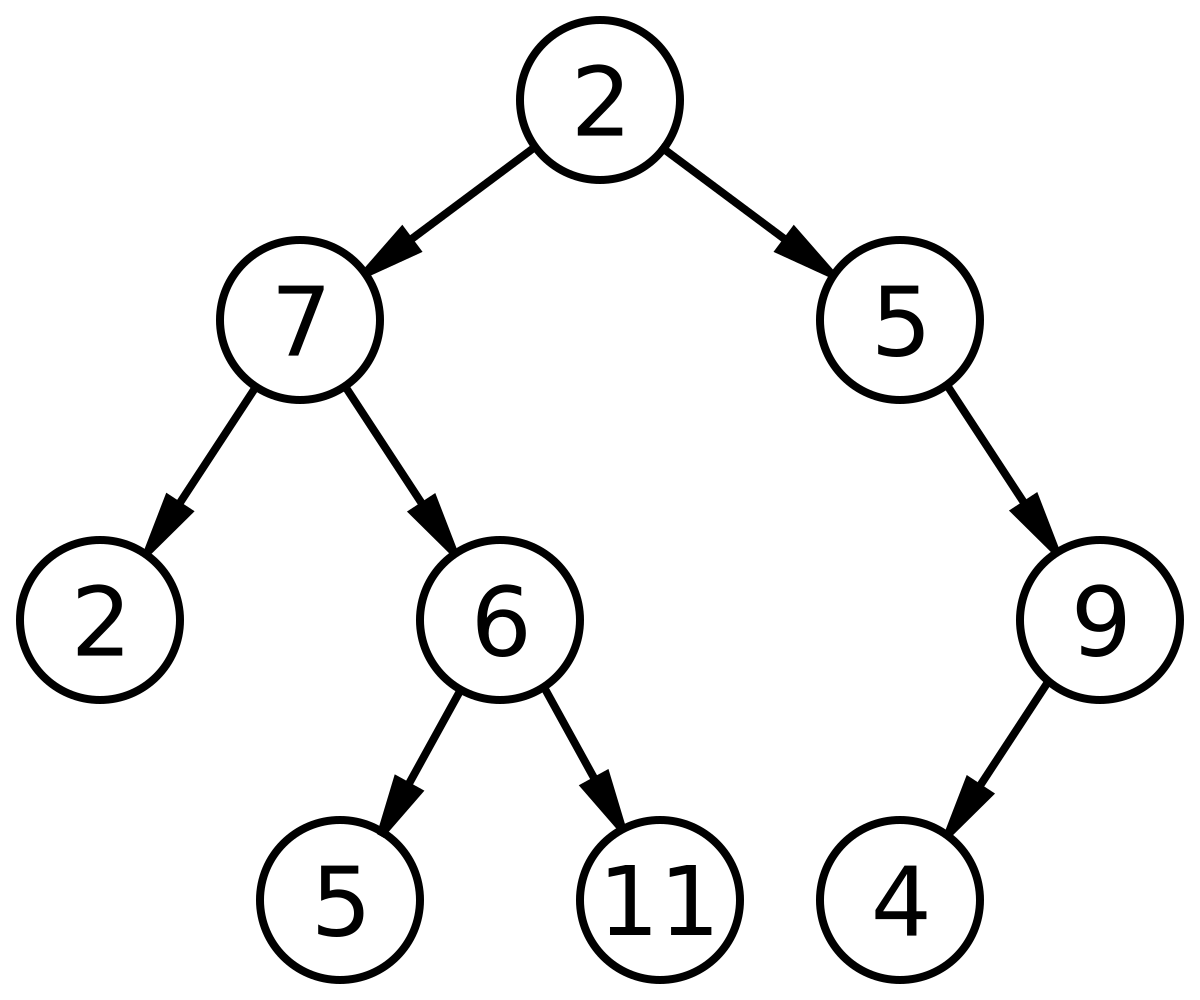
Figure 1. Postorder of this binary tree is 2 5 11 6 7 4 9 5 2
(Source: Wikipedia - Binary tree)
(Source: Wikipedia - Binary tree)
2. Solution
Postorder traversal means we visit the tree in left, right, root order: the left child and right child are visited first, the root is visited last (thus the word post).
3. Implementation
There is a solution that we perform preorder traversal in the order root, right, left, then reverse the result to get the postorder traversal left, right, root. This is trivial and won’t be discussed.
3.1. Recursion
1
2
3
4
5
6
7
void postorder(TreeNode* root) {
if (root == NULL) return;
postorder(root->left);
postorder(root->right);
print("%d ", root->val);
}
Let’s call N is the number of nodes, H is the height of the tree.
- Time complexity: $ O(N)$ since each node is visited exactly once.
- Space complexity: $ O(H)$, the call stack can reach
Hin depth and each recursive call needs $ O(1)$ to store its parameters.
3.2. Iteration
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void postorder(TreeNode* root) {
stack<TreeNode*> stack;
TreeNode* node = root;
while(!stack.empty() || node != NULL) {
if (node != NULL) {
stack.push(node);
node = node->left;
} else {
TreeNode* peek = stack.top();
if (peek->right != NULL && peek->right != lastVisit) {
node = peek->right;
} else {
print("%d ", peek->val); // visit root
stack.pop();
lastVisit = peek;
}
}
}
}
- Time complexity: $ O(N)$ since each node is visited exactly once.
- Space complexity: Space complexity is the maximum size of
stack. On a path from root to some node, easily observe that the stack need to store all of nodes on that path. Thus the space complexity is $ O(H)$.
