Insertion sort

2018-04-22

Content:

1. The idea

Say we want to sort an array in ascending order, N = length of array

The insertion sorting algorithm’s idea is that it slowly get the the part 0..0 (from index 0 to index 0) of the array sorted, then part 0..1 sorted, then part 0..2 sorted.. and finally the whole array 0..(n-1) sorted.

Let’s say we already have the part 0..(i-1) sorted, to have the part 0..i sorted, we insert i-th element to its correct position in the part 0..(i-1) (thus the name insertion sort):

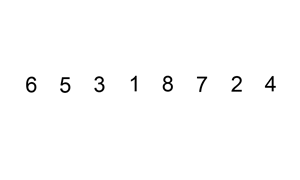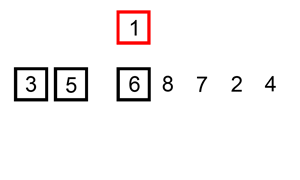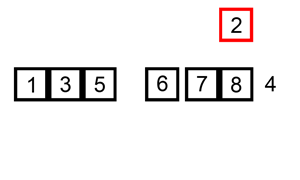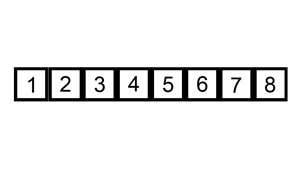
Figure 1. Insertion sort visualization
(Source: Wikipedia - Insertion sort)

2. Implementation

1
2
3
4
5
6
7
8
9
10

void insertion_sort(vector<int>& arr) {
  int n = arr.size();
  for(int k = 1; k < n; k++) {
    int i = k;  // insert arr[i] to 0..(i-1)
    while(i > 0 && a[i-1] > a[i]) {
      swap(a[i-1], a[i]);
      i--;
    }
  }
}

3. Complexity analysis

Let’s call N = length of the array.

Time complexity:

  • In best case: the array is already sorted, complexity is $O(N)$.
  • In average and worst case: $O(N^2)$ (proof is similar to this)

Space complexity: $ O(1)$.

4. Properties

  • Insertion sort is a stable sort algorithm.
  • “When people manually sort cards in a bridge hand, most use a method that is similar to insertion sort” - Wikipedia.
  • ”..insertion sort is one of the fastest algorithms for sorting very small arrays, even faster than quicksort; indeed, good quicksort implementations use insertion sort for arrays smaller than a certain threshold, also when arising as subproblems..” - Wikipedia